+91-9350504919 support@wiredfaculty.com

Sponsor Area

Application Of Derivatives

Question

Wired Faculty App

How fast is the volume of a ball changing with respect to its radius when the radius is 3 m?

Solution

Let V be volume of ball of radius r.

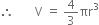
therefore space space space space space space space straight V space equals space 4 over 3 πr cubed

Rate of change of volume with respect to

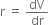
straight r space equals space dV over dr

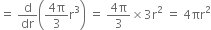
equals space straight d over dr open parentheses fraction numerator 4 straight pi over denominator 3 end fraction straight r cubed close parentheses space equals space fraction numerator 4 straight pi over denominator 3 end fraction cross times 3 straight r squared space equals space 4 πr squared

When r = 3 m, rate of change of volume =

4 space straight pi space left parenthesis 3 right parenthesis squared space equals space 36 space straight pi space space straight m cubed divided by straight m

Some More Questions From Application of Derivatives Chapter

Sponsor Area

Mock Test Series

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation