Sponsor Area
Application Of Derivatives
Question
Find the rate of change of the volume of a ball with respect to its radius r. How fast is the volume changing with respect to the radius when the radius is 2 m?
Solution
Let V be volume of ball of radius r
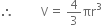
Rate of change of volume with respect to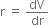
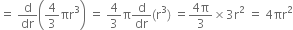
When r = 2 m, rate of change of volume = 4 (2)2 = 16
(2)2 = 16  m3/m.
m3/m.
Rate of change of volume with respect to
When r = 2 m, rate of change of volume = 4
Some More Questions From Application of Derivatives Chapter
Sponsor Area
Mock Test Series
Mock Test Series





