Sponsor Area
Application Of Derivatives
Question
Find the rate of change of the area of a circle with respect to its radius r when
(a) r = 3 cm (b) r = 4 cm
Solution
Let A be area of circle of radius r
Rate of change of area with respect to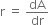
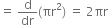
Rate of change of area with respect to
(a) When r = 3, rate of change of area = 2
× 3 = 6 cm2/cm.
(b) When r = 4, rate of change of area = 2 
× 4 = 8 
cm2/cm.
Some More Questions From Application of Derivatives Chapter
The radius of a circle is increasing uniformly at the rate of 4 cm per second Find the rate at which the area of the circle is increasing when the radius is 8 cm.
Sponsor Area
Mock Test Series
Mock Test Series