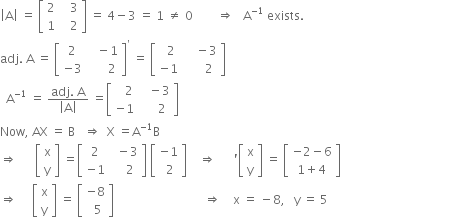+91-8076753736[email protected]
logo
logo
-->

Determinants

Question
CBSEENMA12034732
Wired Faculty App

Use matrix method to solve the system of equations:
2x + 3y = – 1
x + 2y = 2

Solution

The given equations are
2x + 3y = – 1
x + 2y = 2
The equations can be written as
              open square brackets table row 2 cell space space space 3 end cell row 1 cell space space space 2 end cell end table close square brackets space open square brackets table row straight x row straight y end table close square brackets space equals space open square brackets table row cell negative 1 end cell row cell space space 2 end cell end table close square brackets
or      AX space equals space straight B space where space straight A space equals space open square brackets table row 2 cell space space space 3 end cell row 1 cell space space space 2 end cell end table close square brackets comma space space space space space straight A space equals space open square brackets table row straight x row straight y end table close square brackets comma space space straight B space equals space open square brackets table row cell negative 1 end cell row cell space space space 2 end cell end table close square brackets
         open vertical bar straight A close vertical bar space equals space open square brackets table row 2 cell space space space 3 end cell row 1 cell space space space 2 end cell end table close square brackets space equals space 4 minus 3 space equals space 1 space not equal to space 0 space space space space space space space space rightwards double arrow space space space straight A to the power of negative 1 end exponent space exists. adj. space straight A space equals space open square brackets table row 2 cell space space space minus 1 end cell row cell negative 3 end cell cell space space space space space space 2 end cell end table close square brackets to the power of apostrophe space equals space open square brackets table row cell space space 2 end cell cell space space space space minus 3 end cell row cell negative 1 end cell cell space space space space space space 2 end cell end table close square brackets space space straight A to the power of negative 1 end exponent space equals space fraction numerator adj. space straight A over denominator open vertical bar straight A close vertical bar end fraction space equals open square brackets table row cell space space space 2 end cell cell space space space minus 3 end cell row cell negative 1 end cell cell space space space space space 2 end cell end table close square brackets Now comma space AX space equals space straight B space space space rightwards double arrow space space straight X space equals straight A to the power of negative 1 end exponent straight B rightwards double arrow space space space space space space open square brackets table row straight x row straight y end table close square brackets space equals open square brackets table row 2 cell space space minus 3 end cell row cell negative 1 end cell cell space space space space 2 end cell end table close square brackets space open square brackets table row cell negative 1 end cell row cell space 2 end cell end table close square brackets space space space space rightwards double arrow space space space space space space apostrophe open square brackets table row straight x row straight y end table close square brackets space equals space open square brackets table row cell negative 2 minus 6 end cell row cell 1 plus 4 end cell end table close square brackets rightwards double arrow space space space space space open square brackets table row straight x row straight y end table close square brackets space equals space open square brackets table row cell negative 8 end cell row cell space space 5 end cell end table close square brackets space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space rightwards double arrow space space space space straight x space equals space minus 8 comma space space space straight y space equals space 5 space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space

Some More Questions From Determinants Chapter

Mock Test Series

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation