Question
Form the differential equation representing the family of ellipses having foci on x-axis and centre at the origin.
Solution
The general equation of such ellipse is
 ...(1)
...(1)
Differentiating w.r.t. x successively two times, we get.
 ...(2)
...(2)
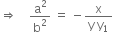 ...(3)
...(3)
and ...(4)
...(4)
From (3), (4), we get

which is the required differential equation.

Differentiating w.r.t. x successively two times, we get.
and
From (3), (4), we get
which is the required differential equation.



