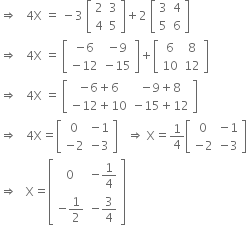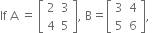$If space straight A space equals space open square brackets table row 2 3 row 4 5 end table close square brackets comma space straight B equals open square brackets table row 3 4 row 5 6 end table close square brackets comma space$ then find a matrix X such that 3A - 2B + 4X=O, where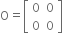 $straight O equals open square brackets table row 0 0 row 0 0 end table close square brackets$

Solution

We have
$straight A equals open square brackets table row 2 3 row 4 5 end table close square brackets comma space straight B equals open square brackets table row 3 4 row 5 6 end table close square brackets$
Now 3A - 2B + 4X = O $rightwards double arrow$ 4X = -3A + 2B
$rightwards double arrow space space space 4 straight X space equals space minus 3 space open square brackets table row 2 3 row 4 5 end table close square brackets plus 2 space open square brackets table row 3 4 row 5 6 end table close square brackets rightwards double arrow space space space 4 straight X space equals space open square brackets table row cell negative 6 end cell cell negative 9 end cell row cell negative 12 end cell cell negative 15 end cell end table close square brackets plus open square brackets table row 6 8 row 10 12 end table close square brackets rightwards double arrow space space space 4 straight X space equals space open square brackets table row cell negative 6 plus 6 end cell cell negative 9 plus 8 end cell row cell negative 12 plus 10 end cell cell negative 15 plus 12 end cell end table close square brackets rightwards double arrow space space space 4 straight X equals open square brackets table row 0 cell negative 1 end cell row cell negative 2 end cell cell negative 3 end cell end table close square brackets space space space rightwards double arrow space straight X equals 1 fourth open square brackets table row 0 cell negative 1 end cell row cell negative 2 end cell cell negative 3 end cell end table close square brackets rightwards double arrow space space space straight X equals open square brackets table row 0 cell negative 1 fourth end cell row cell negative 1 half end cell cell negative 3 over 4 end cell end table close square brackets$

For Daily Free Study Material Join wiredfaculty

Matrices

Some More Questions From Matrices Chapter

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation

Phone Number

Email Address

Loaction