Question
For problem given below, verify that the given function (implicit or explicit) is a solution of the corresponding differential equation:
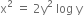 :
: 
Solution
The given differential equation is
 ...(1)
...(1)

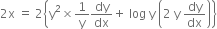
or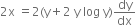


Multiplying both sides by y, we get
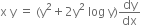
or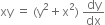

or
Hence the result.
or
Multiplying both sides by y, we get
or
or
Hence the result.



