+91-8076753736[email protected]
logo
logo
-->

Vector Algebra

Question
CBSEENMA12032865
Wired Faculty App

Verify that y - 3 cos (log x) + 4 sin (log x) is a solution of the differential equation 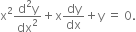straight x squared fraction numerator straight d squared straight y over denominator dx squared end fraction plus straight x dy over dx plus straight y space equals space 0.

Solution

                       straight y space equals space 3 space cos space left parenthesis log space straight x right parenthesis space plus space 4 space sin space left parenthesis log space straight x right parenthesis               ...(1)
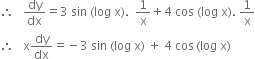
therefore space space space dy over dx equals 3 space sin space left parenthesis log space straight x right parenthesis. space space 1 over straight x plus 4 space cos space left parenthesis log space straight x right parenthesis. space 1 over straight x therefore space space space straight x dy over dx equals negative 3 space sin space left parenthesis log space straight x right parenthesis space plus space 4 space cos thin space left parenthesis log space straight x right parenthesis
Again differentiating w.r.t.x, we get,
               straight x fraction numerator straight d squared straight y over denominator dx squared end fraction plus dy over dx.1 space equals space minus 3 space cos space left parenthesis log space straight x right parenthesis. space 1 over straight x minus space 4 space sin space left parenthesis log space straight x right parenthesis. space 1 over straight x
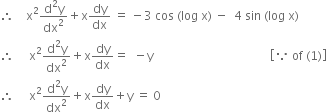
therefore space space space space straight x squared fraction numerator straight d squared straight y over denominator dx squared end fraction plus straight x dy over dx space equals space minus 3 space cos space left parenthesis log space straight x right parenthesis space minus space space 4 space sin space left parenthesis log space straight x right parenthesis therefore space space space space space straight x squared fraction numerator straight d squared straight y over denominator dx squared end fraction plus straight x dy over dx equals space space minus straight y space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space open square brackets because space of space left parenthesis 1 right parenthesis close square brackets therefore space space space space space straight x squared fraction numerator straight d squared straight y over denominator dx squared end fraction plus straight x dy over dx plus straight y space equals space 0
therefore space space space space straight y space equals space 3 space cos space left parenthesis log space straight x right parenthesis space plus space 4 space sin space left parenthesis log space straight x right parenthesis is a solution of the differential equation
                       straight x squared fraction numerator straight d squared straight y over denominator dx squared end fraction plus straight x dy over dx plus straight y space equals space 0.

Some More Questions From Vector Algebra Chapter

Determine order and degree (if defined) of differential equations:
y' + y = ex

Determine order and degree (if defined) of differential equations:
y'' + (y')2 + 2 y = 0

Determine order and degree (if defined) of differential equations:
y″ + 2y′ + sin y = 0

Mock Test Series

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation