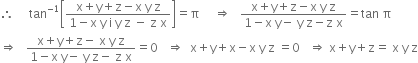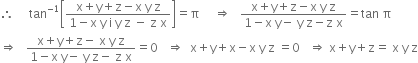If tan–¹.x + tan^–1y + tan ^–1z = $straight pi$ , prove that x + y + z = x y z.

Name: Wired Faculty - The Best Learning App
Rating: 4.6 (1864 reviews)

Solution

∵ tan^–1x + tan^–1y + tan^–1z =

straight pi

therefore space space space space space tan to the power of negative 1 end exponent open square brackets fraction numerator straight x plus straight y plus straight z minus straight x space straight y space straight z over denominator 1 minus straight x space straight y space straight i space straight y space straight z space minus space straight z space straight x end fraction close square brackets equals straight pi space space space space space rightwards double arrow space space space fraction numerator straight x plus straight y plus straight z minus straight x space straight y space straight z over denominator 1 minus straight x space straight y minus space straight y space straight z minus straight z space straight x end fraction equals tan space straight pi rightwards double arrow space space space fraction numerator straight x plus straight y plus straight z minus space straight x space straight y space straight z over denominator 1 minus straight x space straight y minus space straight y space straight z minus space straight z space straight x end fraction equals 0 space space space rightwards double arrow space space straight x plus straight y plus straight x minus straight x space straight y space straight z space equals 0 space space space rightwards double arrow space straight x plus straight y plus straight z equals space straight x space straight y space straight z

For Daily Free Study Material Join wiredfaculty