Question
Prove ![]()
Solution
Put x = sin θ or θ = sin –1x'
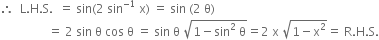
Prove ![]()
Mock Test Series