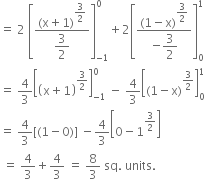Question
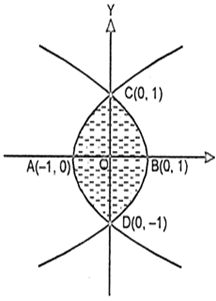
Draw the rough sketch of y2 = x + 1 and y2 = - x + 1 and determine the area enclosed by the two curves.
Solution
The equation of given curves are
y2 - x + 1 ...(1)
and y2 = -x + 1 ...(2)
From (1) and (2), we get,
x + 1 = -x + 1 ⇒ 2 x = 0 ⇒ x = 0
Putting x = 0 in (1). we get,
y2 = 1 or y = -1, 1
∴ points of intersection of given curves are (0, -1) and (0, 1).
Now (1) and (2) represent two parabolas having vertices at (-1, 0) and (1, 0).
Required area = 2 [area CAO + area OBC]
![]()