Question
Using integration, find the area of the triangle ABC whose vertices are A (3, 0) B (4, 5) and C (5, 1).
Solution
The given vertices are A(3, 0), B(4, 5), C(5, 1).
The equation of AB is
![]()
or y = 5x - 5 ...(1)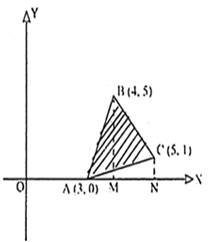
The equation of BC is
![]()
or ![]()
or ![]()
or ![]() ...(2)
...(2)
The equation of CA is
![]()
or ![]() or
or ![]() ...(3)
...(3)
From B. C draw BM. CN ⊥s on x-axis
Required area = Area of ∆AMB + area MNCB — area of ∆ANC
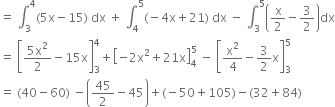
![]()
![]()



