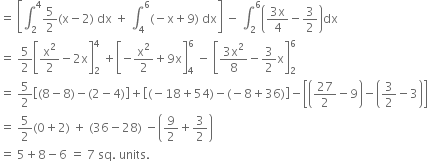Question
Using the method of integration, find the area of the triangle ABC, co-ordinates of whose vertices are A (2, 0), B (4, 5), C (6, 3).
Solution
The equation of AB is
or 
The equation of BC is
or 
The equation of CA is
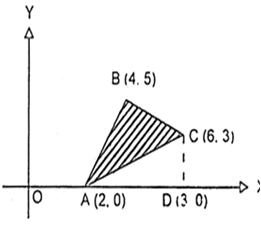
From C, draw CD 
x-axis.
Required area = area of quad. ABCD - area of 
