Question
Find the area of the region enclosed by the parabola x2 = y, the line y = x + 2 and the x-axis.
OR
Draw the rough sketch and find the area of the region:
{(x, y): x2 < y < x + 2}
Solution
The equation of parabola is
x2 = y ...(1)
The equation of line is
y = x + 2 ...(2)
From (1) and (2), we get,
x2 = x + 2
∴ x2 - x - 2 = 0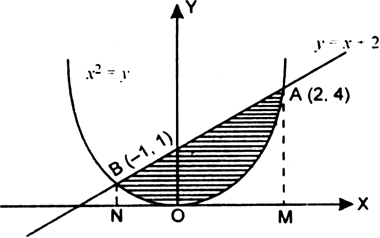
⇒ (x - 2) (x + 1) = 0 ⇒ x = 2, -1
∴ from (2), y= 2 + 2, -1 +2 = 4, 1
∴ parabola (1) meets line (2) in two points A (2, 4) and B (-1. 1).
From A. draw AM ⊥ x-axis and from B. draw BN ⊥ x-axis.
Required area = Area AOB
= ![]()
![]()



