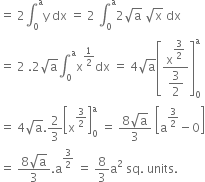Question
Calculate the area bounded by the parabola y2 = 4 a x and its latus rectum.
Solution
The equation of parabola is y2 = 4 a x. ...(1)
Let O be the vertex, S be the focus and LL' be the latus rectum of parabola.
The equation of latus rectum is x = a.
Also, we know that parabola is symmetric about x-axis.

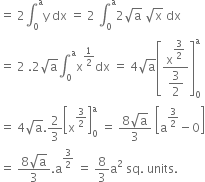
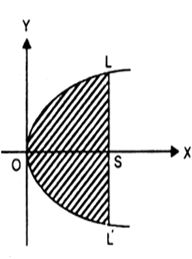
Let O be the vertex, S be the focus and LL' be the latus rectum of parabola.
The equation of latus rectum is x = a.
Also, we know that parabola is symmetric about x-axis.