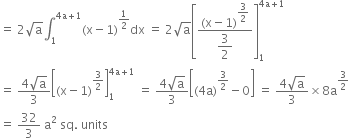Question
Find the area bounded by the curve y2 = 4 a (x-1) and the lines x = 1 and y = 4 a.
Solution
The equation of parabola is y2 = 4 a (x-1) ...(1)
When y = 4 a , from (1) 16 a2 = 4 a (x-1)
⇒ x - 1 = 4 a ⇒ x = 4 a + 1
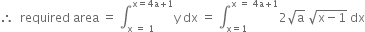

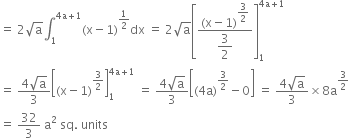
When y = 4 a , from (1) 16 a2 = 4 a (x-1)
⇒ x - 1 = 4 a ⇒ x = 4 a + 1