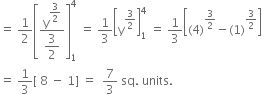Question

Find the area of the region lying in the first quadrant and bounded by y = 4 x², x = 0, y = 1 and y = 4.

Name: Wired Faculty - The Best Learning App
Rating: 4.6 (1864 reviews)

Solution

The equation of parabola is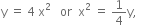

straight y space equals space 4 space straight x squared space space space or space space straight x squared space equals space 1 fourth straight y comma space space

which is upward parabola. The shape of

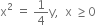straight x squared space equals space 1 fourth straight y comma space space straight x space greater or equal than 0 space

is shown in the figure.

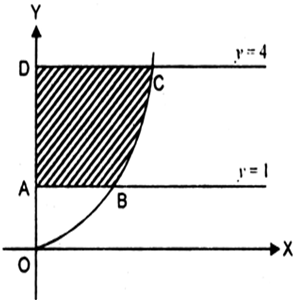
Required area ABCD =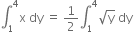

integral subscript 1 superscript 4 straight x space dy space equals space 1 half integral subscript 1 superscript 4 square root of straight y space dy

equals space 1 half open square brackets fraction numerator straight y to the power of begin display style 3 over 2 end style end exponent over denominator begin display style 3 over 2 end style end fraction close square brackets subscript 1 superscript 4 space equals space 1 third open square brackets straight y to the power of 3 over 2 end exponent close square brackets subscript 1 superscript 4 space equals space 1 third open square brackets left parenthesis 4 right parenthesis to the power of 3 over 2 end exponent minus left parenthesis 1 right parenthesis to the power of 3 over 2 end exponent close square brackets equals space 1 third left square bracket space 8 space minus space 1 right square bracket space equals space space 7 over 3 space sq. space units.

For Daily Free Study Material Join wiredfaculty