Sponsor Area
Vector Algebra
Question
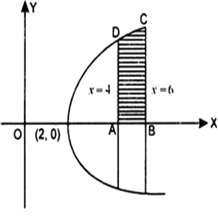
Find the area of the region bounded by y2 = x - 2, x = 4, x = 6 and the x-axis in the first quadrant.
Solution
The equation of curve is y2 = x - 2. which is right handed parabola with vertex at (2, 0).
Two lines are x = 4 and x = 6
Required area = Area ABCD
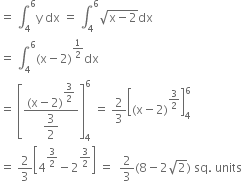
Some More Questions From Vector Algebra Chapter
Sponsor Area
Mock Test Series
Mock Test Series





