Inverse Trigonometric Functions

Show that cos (sin– 1 .x) = sin (cos –1 x) = - Wired Faculty

Question

Show that cos (sin–¹.x) = sin (cos^–1x) = $square root of 1 minus straight x squared end root space for space open vertical bar straight x close vertical bar space space less or equal than space 1$

Solution

Let sin^-1 x=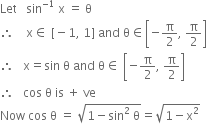 $Let space space space sin to the power of negative 1 end exponent space straight x space equals space straight theta therefore space space space space straight x element of space left square bracket negative 1 comma space 1 right square bracket space and space straight theta element of open square brackets negative straight pi over 2 comma space straight pi over 2 close square brackets therefore space space space straight x equals sin space straight theta space and space straight theta element of space open square brackets negative straight pi over 2 comma space straight pi over 2 close square brackets therefore space space space cos space straight theta space is space plus space ve Now space cos space straight theta space equals space square root of 1 minus sin squared space straight theta end root equals square root of 1 minus straight x squared end root$
[ + ve sign taken before square root]
$therefore space space space cos space left parenthesis sin to the power of negative 1 end exponent straight x right parenthesis equals square root of 1 minus straight x squared end root$

Again, let cos ^–1x = ϕwhere x ∈ [– 1, 1 ] and ϕ ∈ [0,π]
∴ x = cos ϕ where ϕ ∈ [0, π]
∴sin ϕ is + ve

sin space straight ϕ space equals space square root of 1 minus cos squared space straight ϕ end root space equals square root of 1 minus straight x squared end root therefore space space space space sin space left parenthesis cos to the power of negative 1 end exponent straight x right parenthesis equals square root of 1 minus straight x squared end root

(+ ve sign taken before under root)

For Daily Free Study Material Join wiredfaculty