Question
Prove that:![]()
Solution
Let I = ![]()
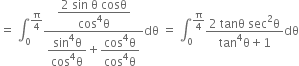
Put tan2 θ = t, ∴ 2 tan θ sec2 θ dθ = dt When θ = 0, t = tan2 0 = 0
When ![]()
![]()
![]()
Prove that:![]()
Let I = ![]()
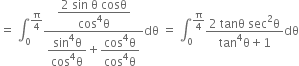
Put tan2 θ = t, ∴ 2 tan θ sec2 θ dθ = dt When θ = 0, t = tan2 0 = 0
When ![]()
![]()
![]()
Mock Test Series