Question
Show that:
Solution
Let I = 
...(1)
Then I = 
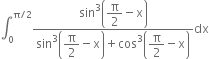
...(2)
Adding (1) and (2), we get,
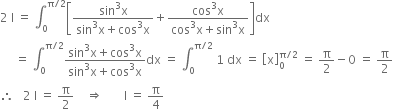
Show that:
Let I = ...(1)
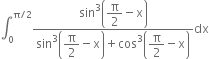
Then I = ...(2)
Adding (1) and (2), we get,
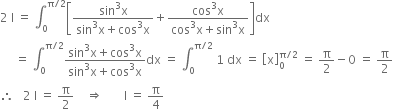
Mock Test Series
