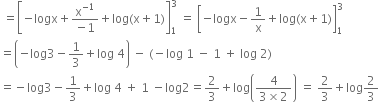Question
Prove the following:![]()
Solution
Let I = ![]()
Put ![]()
Multiplying both sides by x2 (x + 1), we get,
1 ≡ A x (x + 1) + B (x + 1) + C x2 ...(1)
Putting x = 0 in (1), we get,
1 = B, ∴ B = 1
Putting x + 1 = 0 or x = – 1 in (1), we get,
1 = C (– 1 )2, ∴ C = 1
(1) can be written as
1 ≡ A (x2 + x) + B(x + 1) + C x2 ...(2)
Equating coeffs. in (2) of x2, we get,
A + C = 0 ⇒ A + 1 = 0 ⇒ A = – 1![]()
![]()
![]() I =
I = ![]()