Question
Show that the sum of three vector determined by the medians of a triangle directed from the vertices is zero.
Solution
Let D. E. F be the mid-points of the sides BC, CA and AB respectively of ∆ ABC
Now,
[Triangle Law of Vectors]
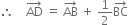...(1)
Again,
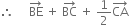...(2)
Also,
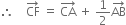...(3)
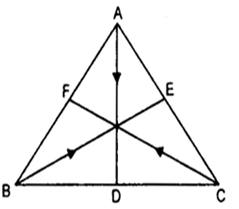
Adding (1), (2) and (3),
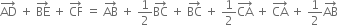
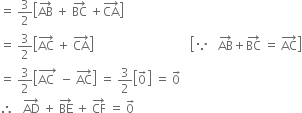
Hence the result.
Now,
[Triangle Law of Vectors] ...(1)Again,
...(2)Also,
...(3)Adding (1), (2) and (3),
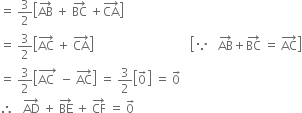
Hence the result.
