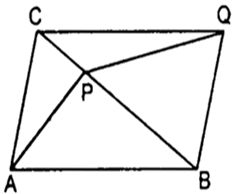
Question
ABC is a triangle and P any point in BC. If 
is the sum of 
show that ABQC is a || gm and Q. therefore a fixed point.
Solution
Here 
(given)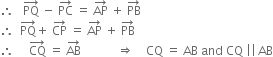
∴ ABQC is a parallelogram
But A. B, C are given to be fixed points and ABQC is a || gm
∴ Q is a fixed point.
