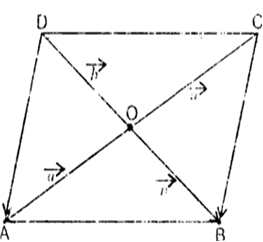
Question
Show that the diagonals a quadrilateral bisect each other if and only if it is a parallelogram.
Solution
Let ABCD be the quadrilateral and O be the point of intersection of the diagonals AC and BD. Let 
. O is the midpoint of both AC and BD if and only if 
or if and only if 
i.e., if any only if 
We also know that a quadrilateral is a parallelogram if and only if its opposite sides are equal and parallel.
Hence the result follows.
