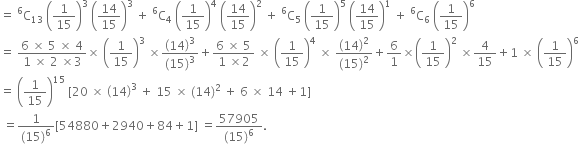Question
Assume that on an average one telephone number out of 15 called between 2 P.M. and 3 P.M. on week days is busy. Why is the probability that if six randomly selected telephone numbers are called, at least three of them will be busy?
Solution
Here n = 6![]()
P(at least three numbers are busy) = P(3) + P(4) + P(5) + P(6)