Question
In a game, a man wins a rupee for a six and loses a rupee for any other number when a fair die is thrown. The man decided to throw a die thrice but to quit as and when he gets a six. Find the expected value of the amount he wins/loses.
Solution
If X is the number of throws, then X may take values 1, 2, 3.
P(X = 1) = P(man gets a six on first throw) =
P(X = 2) = P(man gets a six on first throw but gets a six on second throw)
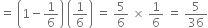
P(X = 3) = P(man does not get a six on first and second throws)
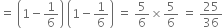
∴ probability distribution of X is
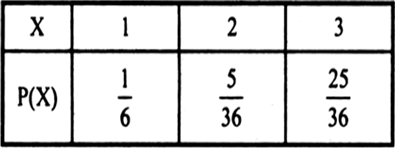
P(X = 1) = P(man gets a six on first throw) =
P(X = 2) = P(man gets a six on first throw but gets a six on second throw)
P(X = 3) = P(man does not get a six on first and second throws)
∴ probability distribution of X is

When X = 1, the man gains Re 1.
When X = 2, the man does not gain anything.
[∵ on first throw he loses Re 1 and on second throw he gains Re 1]
When X = 3,
(i) the man may lose Re 3 when all the three throws show a non-six, which happens with probability ![]()
(ii) the man may lose Re 1 when first two throws show a non-six and third shows a six, which happens with probability ![]()
If Y is the amount gained or lost, then Y takes values 1, 0, - 3, - 1.
∴ probability distribution of Y is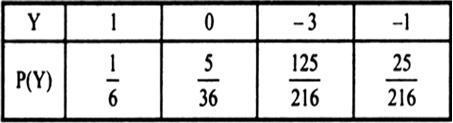
Expected value of Y = ![]()
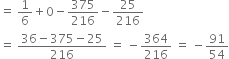
Hence, the man is expected to lose Rs. ![]()



