Question
Suppose that the reliability of HIV test is specified as follows:
Of people having HIV, 90% of the test detect the disease but 10% go undetected. Of people free of HIV, 99% of the test are judged HIV -ve but 1% are diagonsed as showing HIV +ve. From a large population of which only 0.1% have HIV, one person is selected at random, given the HIV test, and the pathologist reports him/her as HIV +ve. What is the probability that the person actually has HIV?
Solution
Let E denote the event that the person selected is actually having HIV and A the event that the person's HIV test is diagnosed as +ve.
Now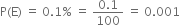

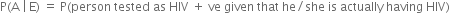
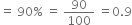
and P(A | E') = P(person tested as HIV +ve given that he/she is actually not having HIV}

Now, by Baye's theorem
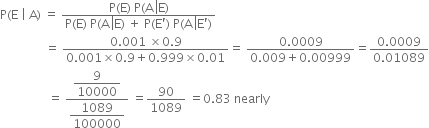
∴ the probability that a person selected at random is actually having HIV given that he/she is tested HIV +ve is 0·083.![]()
Now
and P(A | E') = P(person tested as HIV +ve given that he/she is actually not having HIV}
Now, by Baye's theorem
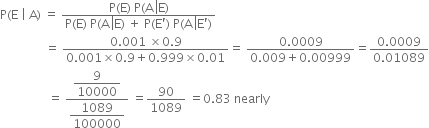
∴ the probability that a person selected at random is actually having HIV given that he/she is tested HIV +ve is 0·083.



