Sponsor Area
Linear Programming
Question
Maximize z = 9 x + 3 y subject to the constraints
2x + 3y ≤ 13
2x + y ≤ 5
x, y ≥ 0
Solution
We have to maximize
z = 9x + 3 y
subject to the constraints
2x + 3 y ≤ 13
2x + y ≤ 5
x, y ≥ 0
Consider a set of rectangular cartesian axes OXY in the plane.
It is clear that any point which satisfies x ≥ 0,y ≥ 0 lies in the first quadrant.
Let us draw the graph of 2x + 3y = 13
For x = 0, 3y = 13 
For y = 0, 2x = 13 
Again we draw the graph of 2x + y = 5
For x = 0, y = 5
For y = 0, 2x = 5 
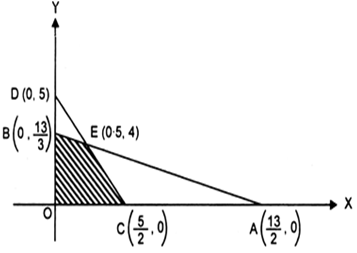
Since feasible region satisfies all the constraints.
OCEB in the feasibe region. The corner points are O(0, 0), 
At O(0, 0), z = 9(0) + 3(0) = 0+ 0 = 0
At 
At 
Some More Questions From Linear Programming Chapter
Solve the following Linear Programming Problems graphically:
Maximise Z = 3x + 2y
subject to the constraints: x + 2y ≤ 10, 3x + y ≤ 15, x, y ≥ 0,
Maximize z = 4x + 1y such that x + 2y ≤ 20, x + y ≤ 15, x ≥ 0, y ≥ 0.
Minimize z = 2x + 3y, such that 1 ≤ x + 2y ≤ 10, x ≥ 0, y ≥ 0.
Solve the following linear programming problem graphically:
Minimise Z = 200x + 500y
subject to the constraints x + 2y ≥ 10, 3x + 4 y ≤ 24, x ≥ 0, y ≥ 0
Solve the following problem graphically:
Minimise and Maximise Z = 3x + 9y
subject to the constraints:
x + 3y ≤ 60
x + y ≥ 10
x ≤ y
x ≥ 0, y ≥ 0
Minimise and Maximise Z = 3x + 9y
subject to the constraints:
x + 3y ≤ 60
x + y ≥ 10
x ≤ y
x ≥ 0, y ≥ 0
Show that the minimum of Z occurs at more than two points.
Minimise and Maximise Z = 5x + 10y subject to constraints x + 2y ≤ 120, x + y ≥ 60, x - 2 y ≥ 0, x, y ≥ 0.
Minimize z = 5x + 7y such that 2x + y ≥ 8, x + 2y ≥ 10, x, y ≥ 0.
Show that the minimum of Z occurs at more than two points.
Minimise and Maximise Z = x + 2y subject to constraints x + 2y ≥ 100, 2x - y ≤ 0, 2x + y ≤ 200, x, y ≥ 0
Sponsor Area
Mock Test Series
Mock Test Series