Question
Find the vector equation of the line passing through (1, 2, 3) and parallel to the planes 
Solution
Let a, b, c be the direction ratios of the line passing through the point (1, 2, 3).
∴ equation of line is
...(1)
The equations of planes are
and
or
and
or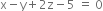
...(2)
and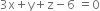
...(3)
Since line (1) is parallel to the plane (2) whose direction ratios of the normal are 1, -1, 2.
∴ a (1) + b (– 1) + c (2) = 0
∴ a – b + 2c = 0
Again line (1) is parallel to the plane (2) whose direction ratios of the normal are 3,1,1.
∴ 3a + b + c = 0 .....(5)
From (4) and (5), we get,
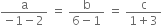
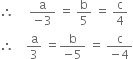
∴ from (1), the equation of line is
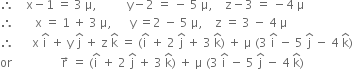
which is vector equation of line.
∴ equation of line is
...(1)The equations of planes are
and
or
and
or
...(2)and
...(3)Since line (1) is parallel to the plane (2) whose direction ratios of the normal are 1, -1, 2.
∴ a (1) + b (– 1) + c (2) = 0
∴ a – b + 2c = 0
Again line (1) is parallel to the plane (2) whose direction ratios of the normal are 3,1,1.
∴ 3a + b + c = 0 .....(5)
From (4) and (5), we get,
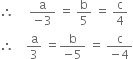
∴ from (1), the equation of line is
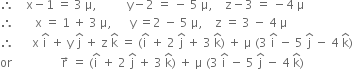
which is vector equation of line.
