Question
Find the equation of the plane passing through the line of intersection of the planes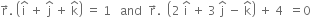 
and parallel to x-axis.
Solution
The equations of the planes are
or
and
or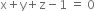
...(1)
and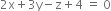
...(2)
Any plane through the intersection of planes (1) and (2) is
(x + y + z – 1) + k (2x + 3y – r + 4) = 0 ...(3)
or (2k + 1) at + (3k + 1) y + (– k + 1) z + (4k – 1) = 0
Its direction ratios are 2k + 1, 3k + 1, – k + 1.
Since plane is parallel to x-axis with direction ratios 1, 0, 0.
∴ 1 (2k + 1) + (0) (3k + 1) + 0 (– k + 1) = 0
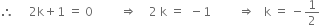
Putting
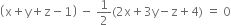
or
or 2x + 2y + 2z – 2 – 2x – 3y + z – 4 = 0
or – y + 3z – 6 = 0
or y - 3z + 6 = 0
Which is required equation of plane.
or
and
or
...(1)and
...(2)Any plane through the intersection of planes (1) and (2) is
(x + y + z – 1) + k (2x + 3y – r + 4) = 0 ...(3)
or (2k + 1) at + (3k + 1) y + (– k + 1) z + (4k – 1) = 0
Its direction ratios are 2k + 1, 3k + 1, – k + 1.
Since plane is parallel to x-axis with direction ratios 1, 0, 0.
∴ 1 (2k + 1) + (0) (3k + 1) + 0 (– k + 1) = 0
Putting
or
or 2x + 2y + 2z – 2 – 2x – 3y + z – 4 = 0
or – y + 3z – 6 = 0
or y - 3z + 6 = 0
Which is required equation of plane.
