Question
Find the equation of the plane which bisects the line joining the points (–1, 2, 3) and (3, – 5 6) at right angles.
Solution
Let A (– 1, 2, 3), B(3, –5, 6) be given points and C be mid-point of AB.
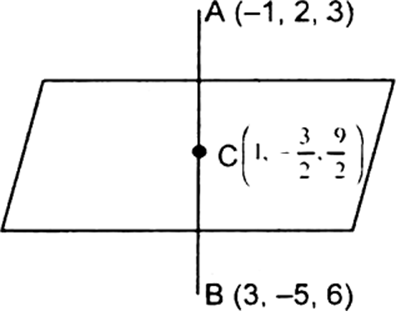
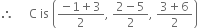
i.e.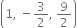
Since the plane passes through the point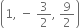
∴ equation of plane is
 ...(1)
...(1)
Direction ratios of AB are 3 + 1, –5 – 2, 6 – 3 i.e. 4, –7, 3.
∴ the line with direction ratios 4, –7, 3 is normal to the plane (1)
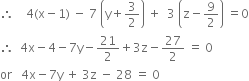
which is required equation of plane.

i.e.
Since the plane passes through the point
∴ equation of plane is
Direction ratios of AB are 3 + 1, –5 – 2, 6 – 3 i.e. 4, –7, 3.
∴ the line with direction ratios 4, –7, 3 is normal to the plane (1)
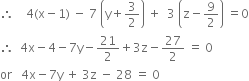
which is required equation of plane.



