Question
If a variable plane at a constant distance p from the origin meets the coordinate axes in points A, B and C respectively. Through these points, planes are drawn parallel to the coordinate planes. Then show that the locus of the point of intersection is
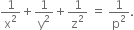
Solution
Let O be the origin and OA = a, OB = b, OC = c
∴ the equation of the plane passing through A, B and C is
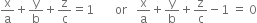
From the given condition,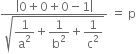
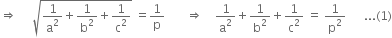
∴ the equation of the plane passing through A, B and C is
From the given condition,
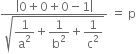
The equation of plane through A (a, 0, 0) parallel to YZ-plane is x = a ... (2)
The equation of plane through B (0, b, 0) parallel to ZX-plane is y = b ... (3)
The equation of plane through C (0, 0, c) parallel to XY-plane is z = c ... (4)
Now to find the locus, we are to eliminate a, b, c.
Putting the values of a, b, c from (2), (3), (4) in (1), we get,![]()



