Question
Find the distance between the point P(6, 5, 9) and the plane determined by the points A(3, –1, 2), B(5, 2, 4) and C(– 1, – 1, 6).
Solution
The equation of plane through the points (3, –1, 2), (5, 2, 4), (– 1, – 1, 6) is

or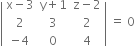
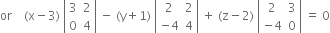
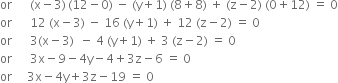
Let p be the perpendicular distance of P(6, 5, 9) from this plane.
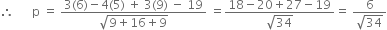

or
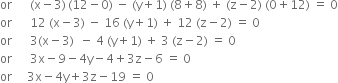
Let p be the perpendicular distance of P(6, 5, 9) from this plane.



