Question
Find the equation of the plane passing through the point (–1, –1, 2) and perpendicular to the planes 3x + 2 y – 3 z = 1 and 5 x – 4 y + z = 5.
Solution
The equation of any plane through (– 1, – 1, 2) is
a (x + 1) + b (y + 1) + c (z – 2) = 0 ....(1)
∴ it is perpendicular to the planes
3 x + 2 y – 3 z = 1 and 5 x – 4 y + z = 5
∴ 3 a + 2 b – 3 c = 0 ....(2)
and 5a – 4 b + c = 0 ...(3)
Solving (2) and (3), we get,
![]()
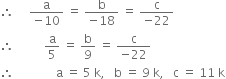
Putting values of a, b, c in (1), we get,
5 k (x + 1) + 9 k (y + 1) + 11 k (z – 2) = 0
or 5 (x + 1) + 9 (y + 1) + 11 (z – 2) = 0
∴ 5x + 9 y + 11 z – 8 = 0 which is required equation of plane.



