Question
Find the equation of the plane passing through the points (2, 3, – 4), (1, –1, 3) and parallel to x-axis.
Solution
The equation of plane through (2, 3, - 4) is
A (x – 2) + B (y – 3) + C (z + 4) = 0 ...(1)
∴ it passes through (1, –1, 3)
∴ A (1 – 2) + B (–1–3) + C (3 + 4) = 0
∴ – A– 4B + 7C = 0
∴ A + 4B – 7C = 0 ...(2)
Now plane (1) is parallel to x-axis.
∴ normal to the plane (1), with direction ratios A, B, C is perpendicular to x-axis with direction ratios 1, 0, 0.
∴ A (1) + B (0) + C (0) = 0
∴ A + 0B + 0C = 0 ...(3)
From (2) and (3), we get,
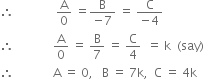
Putting values of A, B, C in (1), we get,
0 (x – 2) + 7k (y – 3) – 4k (z + 4) = 0
or 7 (y – 3) + 4 (z + 4) = 0
or 7 y – 21 + 4z + 16 = 0
or 7 y + 4 z – 5 = 0,
which is required equation of plane.
