Question
Show that the line joining the middle points of two sides of a triangle is parallel to the third side and half of it in length.
Solution
Let A (x1 , y1, z1). B (x2, y2, z2), C (x3, y3, z3) be the vertices of Δ ABC and D, E, F be mid-points of BC, CA and AB respectively.
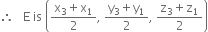
and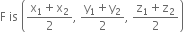

and

Direction-ratios of BC are
x3 – x2, y3 – y2, z3 – z2.
Directions-ratios of FE are
![]()
or ![]()
or ![]()
which are the same as that of BC
∴ FE || BC.
Also,
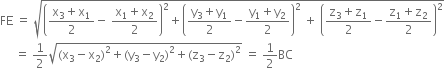
Hence the result.



