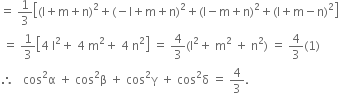A line makes angle α, β, γ and δ with the diagonals of a cube, prove that

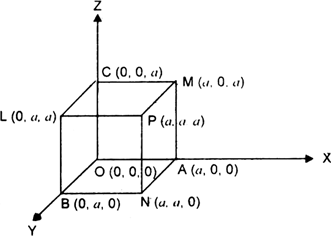
Let OA = OB = OC = a, then the co-ordinates of O , A , B , C are (0, 0, 0), (a, 0, 0), (0, a, 0), (0, 0, a) respectively ; those of P, L, M, N are (a, a, a), (0, a, a), (a, 0, a), (a, a, 0) respectively.
The four diagonals are OP, AL, BM, CN. Direction cosines of OP are proportional to a – 0, a – 0, a – 0, i.e., a, a, a, i.e., 1,1,1.
Direction-cosines of AL are proportional to 0 – a, a – 0, a – 0 i.e., –a, a, a, i.e., – 1, 1, 1.
Direction-cosines of BM are proportional to a – 0, 0 – a, a – 0, i.e., a – a, a i.e., 1, – 1, 1.
Direction-cosines of CN are proportional to a – 0, a – 0, 0 – a i.e., a, a,– a i.e., 1, 1, – 1.
  direction -cosines of OP are 
Directon-cosines of AL are 
Direction-cosines of BM are 
Direction-cosines of CN are 
Let l, m, n be direction-cosines of the line
∴    the line makes an angle α with OP.
              
or                                                          ...(1)
Similarly                                             ...(2)
                                                             ...(3)

Squaring and adding (1), (2), (3) and (4), we get,
cos² α + cos² β + cos² γ + cos² δ