Question
Show that the lines x = ay + b, z = cy + d and x = a' y + b' , z = c' y + d' are perpendicular to each other, if aa' + cc' + 1 = 0.
Solution
The equations of the lines are
x = ay + b, z = cy + d
and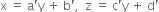
or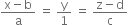
and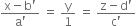
∴ direction ratios of two lines are a, 1, c and a', 1, c'.
The two lines are perpendicular if
(a) (a') + (1) (1) + (c) (c') = 0 [∵ a1 a2 + b1 b2 + c1 c2 = 0]
i.e. if aa' + cc' + 1 = 0
x = ay + b, z = cy + d
and
or
and
∴ direction ratios of two lines are a, 1, c and a', 1, c'.
The two lines are perpendicular if
(a) (a') + (1) (1) + (c) (c') = 0 [∵ a1 a2 + b1 b2 + c1 c2 = 0]
i.e. if aa' + cc' + 1 = 0



