Question
Find a unit normal vector to the plane x + 2y + 3z – 6 = 0.
Solution
The equation of plane is x + 2y’ + 3z – 6 = 0
Direction-ratios of a normal to the plane are 1, 2, 3.
Dividing each by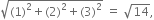
the direction-cosines of a normal to the given plane are 
∴ the normal vector to the given plabne is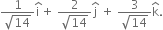
Direction-ratios of a normal to the plane are 1, 2, 3.
Dividing each by
the direction-cosines of a normal to the given plane are ∴ the normal vector to the given plabne is
