Sponsor Area
Three Dimensional Geometry
Question
Find the direction-cosines of a line which makes equal angles with the axes. How many such lines are there?
Solution
Let α be the angle which the line with all the axes,
∴ its direction-cosines are cos α, cos α, cos α
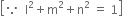
required direction-cosines are 
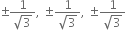
These are four different groups of signs
i.e., +, +, +
+, -, +
+, +, -
+, -, -
∴ there are four distinct lines.
∴ its direction-cosines are cos α, cos α, cos α
required direction-cosines are These are four different groups of signs
i.e., +, +, +
+, -, +
+, +, -
+, -, -
∴ there are four distinct lines.
Some More Questions From Three Dimensional Geometry Chapter
Find the direction cosines of x, y and z-axis.
Sponsor Area
Mock Test Series
Mock Test Series