Sponsor Area
Three Dimensional Geometry
Question
Can a directed line have direction angles 45°, 45°, 60°?
Solution
Let l, m, n be the direction cosines of the line with direction angles 45°, 45°, 60°.

These values of l, m, n do not satisfy the selection l2 + m2 + n2 = 1 as
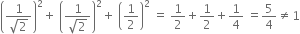
∴ given angles cannot be the direction angles of a line.
These values of l, m, n do not satisfy the selection l2 + m2 + n2 = 1 as
∴ given angles cannot be the direction angles of a line.
Some More Questions From Three Dimensional Geometry Chapter
Find the direction cosines of x, y and z-axis.
Sponsor Area
Mock Test Series
Mock Test Series





