Question
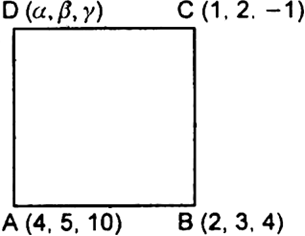
The points A (4, 5, 10), B (2, 3, 4) and C (1, 2, – 1) are three vertices of a parallelogram ABCD. Find vector and cartesian equations for the sides AB and BC and find the coordinates of D.
Solution
A (4, 5, 10), B (2, 3, 4), C (1, 2, – 1) are three vertices of the parallelogram ABCD.

Direction-ratios of AB are 2 – 4, 3 – 5, 4 – 10 i.e.. – 2, – 2, – 6 i.e., 1, 1, 3 and AB passes through A (4, 5, 10)
∴ its vector equation is
![]()
Also Cartesian equations of AB are![]()
Direction ratios of BC are 1– 2, 2 – 3, – 1, – 4
i.e. – 1, – 1, 5 i.e. 1, 1, 5 and BC passes through B (2, 3, 4)
∴ its vector equation is![]()
Also cartesian equations of BC are![]()
Let (α, β, γ) be coordinates of D.
Now mid-points of AC is same as that of BD.