Question
Show that the point whose position vectors are given by 
are collinear.
Solution
Given points have position vectors as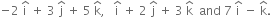 
∴ points are (–2, 3, 5), (1, 2, 3), (7, 0, –1)
The equation of st. line through (–2, 3, 5), (1, 2, 3) is
The point (7, 0, –1) will lie on it
if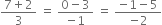
i.e. if 3 = 3 = 3, which is true.
∴ the points (–2, 3, 5), (1, 2, 3) and (7, 0, –1) are collinear.
∴ points with position vectors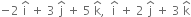
and 
are collinear.
∴ points are (–2, 3, 5), (1, 2, 3), (7, 0, –1)
The equation of st. line through (–2, 3, 5), (1, 2, 3) is
The point (7, 0, –1) will lie on it
if
i.e. if 3 = 3 = 3, which is true.
∴ the points (–2, 3, 5), (1, 2, 3) and (7, 0, –1) are collinear.
∴ points with position vectors
and are collinear.
