Question
Show that the given differential equation is homogeneous and solve it:
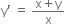
Solution
The given differential equation is
 ...(1)
...(1)
It is a differential equation of the form
Here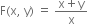
Replacing x by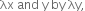 we get,
we get,
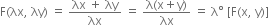
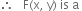 homogeneous function of degree zero.
homogeneous function of degree zero.
 differential equation is a homogeneous differential equation.
differential equation is a homogeneous differential equation.
Put y = v x,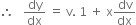
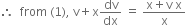
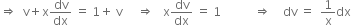
Integrating,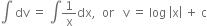
or
It is a differential equation of the form
Here
Replacing x by
Put y = v x,
Integrating,
or



