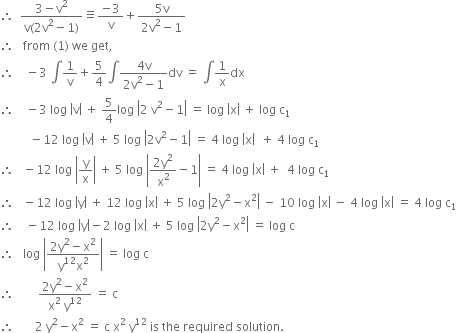Question
Show that the following differential equation is homogeneous and find a primitive of it. Derive the solution wherever possible:
Solution
The given differential equation is
or 
Put y = v x so that 
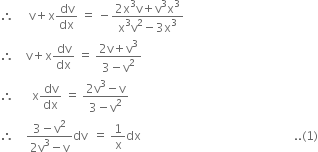
Put 
...(2)
Put v = 0 in (2)
Equating coefficients in (2) of
-1 = 2 A + B 
