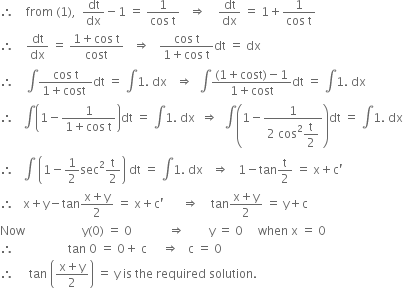+91-8076753736[email protected]
logo
logo
-->

Differential Equations

Question
CBSEENMA12033101
Wired Faculty App

Solve the following initial value problem
cos (x + y) dy = dx, y (0) = 0

Solution
The given differential equation is
                    cos space left parenthesis straight x plus straight y right parenthesis space dy space equals space dx space space space space or space space space space dy over dx space equals space fraction numerator 1 over denominator cos space left parenthesis straight x plus straight y right parenthesis end fraction               ...(1)
Put x + y = t,        therefore space space space 1 plus dy over dx equals dt over dx space space or space space dy over dx space equals space dt over dx minus 1
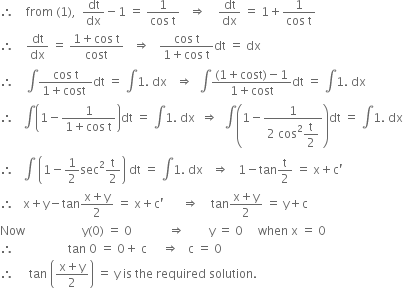
therefore space space space space from space left parenthesis 1 right parenthesis comma space space dt over dx minus 1 space equals space fraction numerator 1 over denominator cos space straight t end fraction space space space rightwards double arrow space space space space dt over dx space equals space 1 plus fraction numerator 1 over denominator cos space straight t end fraction therefore space space space space dt over dx space equals space fraction numerator 1 plus cos space straight t over denominator cost end fraction space space space rightwards double arrow space space space fraction numerator cos space straight t over denominator 1 plus cos space straight t end fraction dt space equals space dx therefore space space space space integral fraction numerator cos space straight t over denominator 1 plus cost space end fraction dt space equals space integral 1. space dx space space space rightwards double arrow space space integral fraction numerator left parenthesis 1 plus cost right parenthesis minus 1 over denominator 1 plus cost end fraction dt space equals space integral 1. space dx therefore space space space integral open parentheses 1 minus fraction numerator 1 over denominator 1 plus cos space straight t end fraction close parentheses dt space equals space integral 1. space dx space space rightwards double arrow space space integral open parentheses 1 minus fraction numerator 1 over denominator 2 space cos squared begin display style straight t over 2 end style end fraction close parentheses dt space equals space integral 1. space dx therefore space space space integral space open parentheses 1 minus 1 half sec squared straight t over 2 close parentheses space dt space equals space integral 1. space dx space space space rightwards double arrow space space space 1 minus tan straight t over 2 space equals space straight x plus straight c apostrophe therefore space space space straight x plus straight y minus tan fraction numerator straight x plus straight y over denominator 2 end fraction space equals space straight x plus straight c apostrophe space space space space space space rightwards double arrow space space space space tan fraction numerator straight x plus straight y over denominator 2 end fraction space equals space straight y plus straight c Now space space space space space space space space space space space space space space space space space space space straight y left parenthesis 0 right parenthesis space equals space 0 space space space space space space space space space space space space rightwards double arrow space space space space space space space space straight y space equals space 0 space space space space space when space straight x space equals space 0 therefore space space space space space space space space space space space space space space space space space space tan space 0 space equals space 0 plus space straight c space space space space space rightwards double arrow space space space straight c space equals space 0 therefore space space space space space tan space open parentheses fraction numerator straight x plus straight y over denominator 2 end fraction close parentheses space equals space straight y space is space the space required space solution. space

Some More Questions From Differential Equations Chapter

Mock Test Series

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation