Question
Find one-parameter families of solution curves of the following differential equation:
![]()
Solution
The given differential equation is
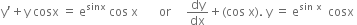
Comparing it with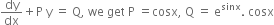

Solution of given differential equation is
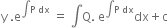
or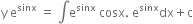
or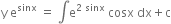 ...(1)
...(1)
Let I =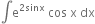
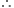
Put sinx = t,
 I =
I = 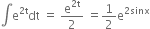
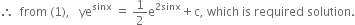
Comparing it with
Solution of given differential equation is
or
or
Let I =
Put sinx = t,



