Question
Find a particular solution of the differential equation
(x – y) (dx + dy) = dx – dy. given that y = – 1, when x = 0.
Solution
The given differential equation is
(x – y) (dx + dy) = dx – dy ...(1)
or
Integrating, we get
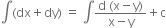
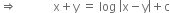....(2)
Now x = 0, y = -1
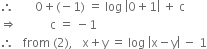
which is required solution.
(x – y) (dx + dy) = dx – dy ...(1)
or
Integrating, we get
....(2)Now x = 0, y = -1
which is required solution.
