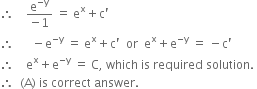Question

The general solution of the differential equation 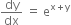$dy over dx space equals space straight e to the power of straight x plus straight y end exponent$ is
e^x + e^{– y} = C
e^x+ e^y = C
e^{– x} + e^y = C
e^{– x}+ e^–y = C

Name: Wired Faculty - The Best Learning App
Rating: 4.6 (1864 reviews)

Solution

e^x + e^{– y} = C The given differential equation is

dy over dx space equals space straight e to the power of straight x plus straight y end exponent space space space space space or space space dy over dx space equals space straight e to the power of straight x. space straight e to the power of straight y

Separating the variables, we get,

1 over straight e to the power of straight y dy space equals space straight e to the power of straight x space dx

Integrating,

integral straight e to the power of negative straight y end exponent dy space equals space integral straight e to the power of straight x space dx

WiredFaculty

For Daily Free Study Material Join wiredfaculty